Learn how to effectively Solving Equations with Degrees our comprehensive guide. Discover expert tips, strategies, and tools for mastering degree equation solver techniques.
Solving equations with degrees can often be a daunting task, but with the right approach and understanding, it becomes much more manageable. Whether you’re a student grappling with trigonometric equations or a professional dealing with complex mathematical problems, mastering the art of Solving Equations with Degrees. In this guide, we’ll delve into various methods, tips, and tricks to empower you to tackle degree equations with confidence.
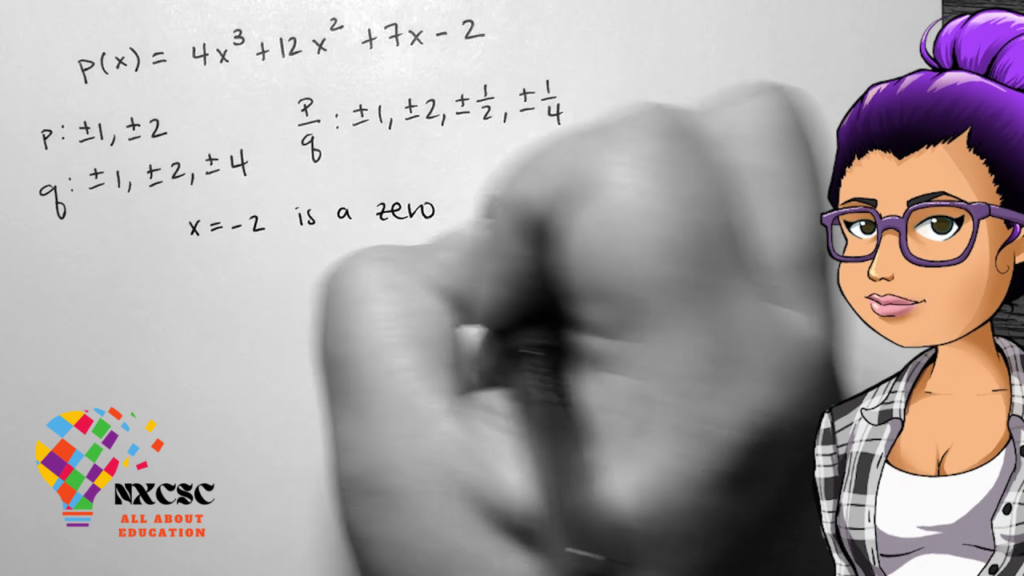
Understanding Solving Equations with Degrees
To embark on our journey of mastering degree equation solving, it’s crucial to first understand what degree equations entail. Degree equations are mathematical expressions involving variables raised to powers, typically expressed in degrees. These equations can range from simple linear equations to intricate polynomial equations with multiple variables.
Also Must Read: How to get an audible daily deal
Exploring Different Types of Degree Equations
Degree equations come in various forms, each requiring a unique approach for solving. Let’s explore some common types:
- Linear Equations: These equations involve variables raised to the power of 1 and are relatively straightforward to solve.
- Quadratic Equations: Quadratic equations feature variables raised to the power of 2, often requiring factoring or quadratic formula application.
- Cubic Equations: Cubic equations involve variables raised to the power of 3 and may necessitate advanced techniques like synthetic division or the cubic formula.
Strategies for Solving Degree Equations
Successfully solving degree equations demands a strategic approach and familiarity with proven methods. Here are some effective strategies to employ:
1. Substitution Method
The substitution method involves replacing one variable with an expression containing other variables, simplifying Solving Equations with Degrees and facilitating solution discovery.
2. Factoring
Factoring entails breaking down equations into smaller, manageable components, often revealing solutions more readily.
3. Quadratic Formula
For quadratic equations, the quadratic formula serves as a reliable tool for determining solutions without factoring.
4. Completing the Square
Completing the square involves transforming quadratic equations into perfect square trinomials, simplifying the solving process.
Common Challenges and How to Overcome Them
While tackling Solving Equations with Degrees, you may encounter various hurdles. Here are some common challenges and strategies for overcoming them:
1. Complex Expressions
Complex expressions within degree equations can complicate the solving process. To overcome this challenge, break down the equation into smaller components and tackle each part individually.
2. Multiple Variables
Equations with multiple variables require careful consideration and possibly the application of advanced techniques like simultaneous equations or substitution.
3. Irrational Solutions
Some degree equations may yield irrational solutions Solving Equations with Degrees , which can be challenging to interpret. Ensure thorough understanding of the problem context and verify solutions meticulously.
Practical Applications of Degree Equation Solver Techniques
Degree equation solver techniques find widespread applications across various fields, including:
- Engineering: Engineers utilize degree equation solving to analyze and design structural components, electrical circuits, and mechanical systems.
- Physics: Physicists employ degree equations to model and predict phenomena such as projectile motion, harmonic oscillation, and fluid dynamics.
- Finance: Financial analysts leverage equation solving to assess investment strategies, risk factors, and economic trends.
Degree Equation Solver Tools and Resources
In the digital age, an array of degree equation solver tools and resources are readily accessible. Some notable options include:
- Online Equation Solvers: Websites offering interactive platforms for inputting and solving degree equations.
- Mathematical Software: Robust software packages like MATLAB, Mathematica, and Maple equipped with advanced equation solving capabilities.
- Educational Platforms: Online courses, tutorials, and textbooks dedicated to mathematical problem-solving techniques.
Degree Equation Solver: FAQs
How do I determine the degree of an equation?
- To determine the degree of an equation, identify the highest power to which any variable is raised.
Can all degree equations be solved algebraically?
- Not necessarily. Some degree equations may have solutions that cannot be expressed algebraically and require numerical approximation methods.
What are the practical implications of solving degree equations?
- Solving degree equations enables us to model real-world phenomena, make predictions, and solve complex problems across various disciplines.
Are there any online resources for practicing degree equation solving?
- Yes, several online platforms offer practice problems, tutorials, and interactive tools for honing degree equation solving skills.
How can I verify the solutions obtained for degree equations?
- You can verify solutions by substituting them back into the original equation and ensuring that they satisfy all conditions.
Is it possible to encounter extraneous solutions when solving degree equations?
- Yes, extraneous solutions may arise, especially when certain operations, such as squaring both sides of an equation, are performed.
Conclusion
Mastering the art of Solving Equations with Degrees is a valuable skill with far-reaching applications in various domains. By understanding the fundamentals, employing effective strategies, and leveraging available resources, you can confidently tackle degree equations and unlock new avenues of problem-solving proficiency.
Also Must Read: Degree Accounting 1st Paper

